티스토리 뷰
# 파이썬 ≥3.5 필수
import sys
assert sys.version_info >= (3, 5)
# 사이킷런 ≥0.20 필수
import sklearn
assert sklearn.__version__ >= "0.20"
# 텐서플로 ≥2.0 필수
import tensorflow as tf
from tensorflow import keras
assert tf.__version__ >= "2.0"
if not tf.config.list_physical_devices('GPU'):
print("감지된 GPU가 없습니다. GPU가 없으면 LSTM과 CNN이 매우 느릴 수 있습니다.")
# 공통 모듈 임포트
import numpy as np
import os
# 노트북 실행 결과를 동일하게 유지하기 위해
np.random.seed(42)
tf.random.set_seed(42)
# 깔끔한 그래프 출력을 위해
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
plt.style.use('default')
def plot_series(series,
y=None,
y_pred=None,
x_label="$t$",
y_label="$x(t)$",
legend=True):
plt.plot(series, ".-")
if y is not None:
plt.plot(n_steps, y, "bo", label="Target")
if y_pred is not None:
plt.plot(n_steps, y_pred, "rx", markersize=10, label="Prediction")
plt.grid(True)
if x_label:
plt.xlabel(x_label, fontsize=16)
if y_label:
plt.ylabel(y_label, fontsize=16, rotation=0)
plt.hlines(0, 0, 100, linewidth=1)
plt.axis([0, n_steps + 1, -1, 1])
if legend and (y or y_pred):
plt.legend(fontsize=14, loc="upper left")
RNN과 CNN을 사용한 시퀸스 처리¶
이제는 순환 신경망이다. 그동안은 신호가 한 방향으로 흘렀지만 이제는 뒤쪽으로도 흐른다.
게다가 고정된 길이를 가진 입력뿐만 아니라 임의의 길이를 가지는 시퀸스 데이터를 처리할 수 있다.
예를 들면 문장, 문서, 오디오와 같은 데이터를 입력으로 받을 수 있고 자연어 처리에도 유용하다.
순환 뉴런과 순환 층¶
RNN을 일고 있는 순환 뉴런들은 각 타임 스텝 $t$ 마다 현재 타입 스텝의 입력 $x_{(t)}$ 뿐만 아니라
이전 타임 스텝의 출력 $y_{(t-1)}$을 입력으로 받는다.
각 순환 뉴런은 그렇기에 현재 타입 스텝의 입력 $x_{(t)}$ 에 대한 가중치 $W_x$ 와
이전 타임 스텝의 출력 $y_{(t-1)}$ 에 대한 가중치 $W_y$ 를 가지게 된다.
이를 식을 통해 전체 순환 층의 출력에 대해 표시하면 다음과 같이 나타낼 수 있다.
\begin{equation} y_{(t)} = \phi\;(\;W_x^T x_{(t)}\;+\;W_y^T y_{(t-1)}+b\;) \end{equation}
그리고 매 타입스텝 $t$ 에 대한 모든 입력을 행렬 $X_{(t)}$ 로 만들어 미니배치 전체에 대해 나타내면
\begin{align*} Y_{(t)} & = \phi\;(\;X_{(t)}W_x\;+\;Y_{(t-1)}W_y\;+b\;) \\ & = \phi\;(\;[X_{(t)}\;Y_{(t-1)}]\;W\;+b\;) \quad where\;W = \begin{bmatrix} W_x \\ W_y \end{bmatrix} \end{align*}
메모리 셀¶
타임 스텝 $t$ 에서 순환 뉴런의 출력은 이전 타임 스텝의 모든 입력에 대한 함수이기도 하다.
따라서 어떤 상태를 보존하는 일종의 메모리 형태로 볼 수 있으며 이런 신경망 구성 요쇼를 메모리 셀 이라고 부른다.
보통 10스텝 정도로 짧은 패턴을 기억할 수 있는 기본적인 셀이다.
일반적으로 타임 스텝 $t$ 에서 셀의 상태인 $h(t)$ 는 현재 스텝의 입력과 이전 스텝의 상태에 대한 함수이다.
따라서 $h(t)=f(\ h_{(t-1)},\;x_{(t)}\ )$ 로 나타낼 수 있고 왠만하면 출력 값인 $y(t)$ 와 동일하다.
(물론 다음 사진과 같이 복잡한 셀에서는 그러지 않을 수 있다)
입력과 출력 시퀸스¶
RNN은 입력 시퀸스를 받아서 출력 시퀸스를 만들 수 있다.
예를 들어 최근 N일간의 주식 가격을 입력값으로 받아 각 입력값보다 하루 앞선 가격을 예측하여 출력할 수 있다.
이를 시퀸스-투-시퀸스 (Sequence-to-Sequence Network) 라고 부른다.
아니면 입력값은 시퀸스로 받더라도 출력값은 하나의 벡터값으로 출력할 수 있다.
예를 들면 영화 리뷰 문장(시퀸스)을 보고 영화에 대한 호감도를 -1에서 1까지의 점수(벡터값)로 나타낸다.
이를 시퀸스-투-벡터 (Sequence-to-Vector Network) 라고 부른다.
반대로 첫 타임 스텝에 하나의 벡터를 입력값으로 넘겨주고 출력값으로 하나의 시퀸스를 얻을 수 있다.
예를 들면 이미지를 입력하여 이미지에 대한 캡션을 출력할 수 있다.
이를 벡터-투-시퀸스(Vector-to-Sequence Network) 라고 부른다
그리고 인코더 라고 부르는 Sequence-to-Vector 네트워크가 특정 문장을 하나의 벡터로 인코딩하고
디코더 라고 부르는 Vector-to-Sequence 네트워크를 통해 해당 벡터를 다른 언어로 번역하는데 이용할 수 있다.
이처럼 인코더-디코더 라고 불리는 이중 단계 모델 은 하나의 시퀸스-시퀸스 RNN 모델보다 잘 작동된다.

RNN 훈련하기¶
RNN 또한 역전파를 이용하여 훈련된다. RNN을 타임 스텝으로 펼치고 출력값을 기준으로 역전파를 전달한다.
이를 BPTT (BackPropagation Through Time) 라고 한다.

우선 해당 사진처럼 출력 값들(비용 함수는 일부 출력을 무시해도 된다)을 기준으로 비용 함수를 계산한다.
그레디언트 자체는 일부 출력을 기준으로 흐르지만 네트워크를 따라 역방향으로 전파되며 파라미터를 업데이트 시킨다.
시계열 예측¶
시간당, 날짜별 데이터와 같이 타임 스텝마다 하나 이상의 값을 가진 시퀸스 데이터들을 시계열(time series) 데이터라고 부른다.
타임 스텝마다 하나의 값을 가지면 단변량 시계열(univariate time series)이고,
하나 이상의 값을 가지게 되면 다변량 시계열 (multivariate time series)라고 부른다.
RNN을 통하여서 우리는 미래의 값을 예측하거나 누락된 값을 채운다.
def generate_time_series(batch_size, n_steps):
freq1, freq2, offsets1, offsets2 = np.random.rand(4, batch_size, 1)
time = np.linspace(0, 1, n_steps)
series = 0.5 * np.sin((time - offsets1) * (freq1 * 10 + 10)) # 웨이브 1
series += 0.2 * np.sin((time - offsets2) * (freq2 * 20 + 20)) # + 웨이브 2
series += 0.1 * (np.random.rand(batch_size, n_steps) - 0.5) # + 잡음
return series[..., np.newaxis].astype(np.float32)
보통 시계열 데이터의 형상은 (배치 크기, 타임 스텝 수, 차원 수) 로 나타낸다.
단변량의 경우 차원 수가 1이 되고 다변량의 경우 1 이상의 수를 가지게 된다.
n_steps = 50
series = generate_time_series(10000, n_steps + 1)
X_train, y_train = series[:7000, :n_steps], series[:7000, -1]
X_valid, y_valid = series[7000:9000, :n_steps], series[7000:9000, -1]
X_test, y_test = series[9000:, :n_steps], series[9000:, -1]
X_train.shape
(7000, 50, 1)기준 성능¶
기준 성능을 미리 준비하여 모델의 성능을 평가할 때 성능이 나쁜지를 판단하자
각 시계열 데이터의 마지막 값을 바로 이전값으로 그대로 예측하는 것을 순진한 예측(naive forecasting)이라고 부른다.
# 마지막 시계열 값을 그대로 결과값으로 이용한다.
y_pred = X_valid[:,-1]
np.mean(keras.losses.mean_squared_error(y_valid,y_pred))
0.020211367또는 FCN을 사용하여 구현하는 방법도 있다.
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[50,1]),
keras.layers.Dense(1)
])
model.compile(loss="mse", optimizer="adam",metrics="mse")
history = model.fit(X_train,y_train,validation_data=(X_valid,y_valid),epochs=20)
Epoch 1/20
219/219 [==============================] - 2s 2ms/step - loss: 0.1001 - mse: 0.1001 - val_loss: 0.0545 - val_mse: 0.0545
Epoch 2/20
219/219 [==============================] - 0s 2ms/step - loss: 0.0379 - mse: 0.0379 - val_loss: 0.0266 - val_mse: 0.0266
Epoch 3/20
219/219 [==============================] - 0s 2ms/step - loss: 0.0202 - mse: 0.0202 - val_loss: 0.0157 - val_mse: 0.0157
Epoch 4/20
219/219 [==============================] - 0s 2ms/step - loss: 0.0131 - mse: 0.0131 - val_loss: 0.0116 - val_mse: 0.0116
Epoch 5/20
219/219 [==============================] - 0s 1ms/step - loss: 0.0103 - mse: 0.0103 - val_loss: 0.0098 - val_mse: 0.0098
Epoch 6/20
219/219 [==============================] - 0s 2ms/step - loss: 0.0089 - mse: 0.0089 - val_loss: 0.0087 - val_mse: 0.0087
Epoch 7/20
219/219 [==============================] - 0s 2ms/step - loss: 0.0080 - mse: 0.0080 - val_loss: 0.0079 - val_mse: 0.0079
Epoch 8/20
219/219 [==============================] - 0s 2ms/step - loss: 0.0073 - mse: 0.0073 - val_loss: 0.0071 - val_mse: 0.0071
Epoch 9/20
219/219 [==============================] - 0s 2ms/step - loss: 0.0066 - mse: 0.0066 - val_loss: 0.0066 - val_mse: 0.0066
Epoch 10/20
219/219 [==============================] - 0s 2ms/step - loss: 0.0061 - mse: 0.0061 - val_loss: 0.0062 - val_mse: 0.0062
Epoch 11/20
219/219 [==============================] - 0s 2ms/step - loss: 0.0057 - mse: 0.0057 - val_loss: 0.0057 - val_mse: 0.0057
Epoch 12/20
219/219 [==============================] - 0s 2ms/step - loss: 0.0054 - mse: 0.0054 - val_loss: 0.0055 - val_mse: 0.0055
Epoch 13/20
219/219 [==============================] - 0s 2ms/step - loss: 0.0052 - mse: 0.0052 - val_loss: 0.0052 - val_mse: 0.0052
Epoch 14/20
219/219 [==============================] - 0s 2ms/step - loss: 0.0049 - mse: 0.0049 - val_loss: 0.0049 - val_mse: 0.0049
Epoch 15/20
219/219 [==============================] - 0s 2ms/step - loss: 0.0048 - mse: 0.0048 - val_loss: 0.0048 - val_mse: 0.0048
Epoch 16/20
219/219 [==============================] - 0s 2ms/step - loss: 0.0046 - mse: 0.0046 - val_loss: 0.0048 - val_mse: 0.0048
Epoch 17/20
219/219 [==============================] - 0s 2ms/step - loss: 0.0045 - mse: 0.0045 - val_loss: 0.0045 - val_mse: 0.0045
Epoch 18/20
219/219 [==============================] - 0s 2ms/step - loss: 0.0044 - mse: 0.0044 - val_loss: 0.0044 - val_mse: 0.0044
Epoch 19/20
219/219 [==============================] - 0s 2ms/step - loss: 0.0043 - mse: 0.0043 - val_loss: 0.0043 - val_mse: 0.0043
Epoch 20/20
219/219 [==============================] - 0s 2ms/step - loss: 0.0042 - mse: 0.0042 - val_loss: 0.0042 - val_mse: 0.0042
model.evaluate(X_test,y_test)
32/32 [==============================] - 0s 1ms/step - loss: 0.0042 - mse: 0.0042
[0.004241826478391886, 0.004241826478391886]심층 RNN¶
RNN 을 이용하는 경우에서는 셀을 여러 층으로 쌓는 거의 일반적이다. 이를 심층 RNN 이라고 부른다.
return_sequences=False 를 사용하면 모든 타임스텝에서 나온 세퀸스가 아닌 마지막 출력만 이용한다.
중간에는 True로 두어서 다음 RNN이 세퀸스 데이터를 받을 수 있도록 하자.
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None, 1]),
keras.layers.SimpleRNN(20, return_sequences=True),
keras.layers.SimpleRNN(1)
])
model.compile(loss="mse",optimizer="nadam")
history = model.fit(X_train,y_train, epochs=10, validation_data = (X_valid,y_valid))
Epoch 1/10
219/219 [==============================] - 18s 77ms/step - loss: 0.0489 - val_loss: 0.0123
Epoch 2/10
219/219 [==============================] - 16s 74ms/step - loss: 0.0079 - val_loss: 0.0058
Epoch 3/10
219/219 [==============================] - 16s 73ms/step - loss: 0.0058 - val_loss: 0.0046
Epoch 4/10
219/219 [==============================] - 16s 72ms/step - loss: 0.0049 - val_loss: 0.0050
Epoch 5/10
219/219 [==============================] - 16s 72ms/step - loss: 0.0045 - val_loss: 0.0041
Epoch 6/10
219/219 [==============================] - 16s 74ms/step - loss: 0.0040 - val_loss: 0.0036
Epoch 7/10
219/219 [==============================] - 16s 72ms/step - loss: 0.0038 - val_loss: 0.0038
Epoch 8/10
219/219 [==============================] - 16s 71ms/step - loss: 0.0037 - val_loss: 0.0034
Epoch 9/10
219/219 [==============================] - 16s 72ms/step - loss: 0.0036 - val_loss: 0.0033
Epoch 10/10
219/219 [==============================] - 17s 77ms/step - loss: 0.0035 - val_loss: 0.0032
단변량 시계열을 예측하기에 마지막에 하나의 출력값이 필요하다.
굳이 이 과정에서 SimpleRNN을 사용해줄 필요는 없고 tanh 함수 때문에 값이 -1과 1사이에 바운딩 된다.
따라서 다른 활성화 함수를 사용하기 위해 Dense layer로 변경하는 경우가 많다.
이를 위해 2번째 layer의 return_sequences를 지워주자.
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None, 1]),
keras.layers.SimpleRNN(20),
keras.layers.Dense(1)
])
model.compile(loss="mse",optimizer="adam")
history = model.fit(X_train,y_train, epochs=20, validation_data = (X_valid,y_valid))
Epoch 1/20
219/219 [==============================] - 12s 51ms/step - loss: 0.0232 - val_loss: 0.0052
Epoch 2/20
219/219 [==============================] - 10s 46ms/step - loss: 0.0043 - val_loss: 0.0036
Epoch 3/20
219/219 [==============================] - 10s 46ms/step - loss: 0.0035 - val_loss: 0.0031
Epoch 4/20
219/219 [==============================] - 10s 47ms/step - loss: 0.0033 - val_loss: 0.0033
Epoch 5/20
219/219 [==============================] - 10s 46ms/step - loss: 0.0033 - val_loss: 0.0034
Epoch 6/20
219/219 [==============================] - 10s 45ms/step - loss: 0.0031 - val_loss: 0.0029
Epoch 7/20
219/219 [==============================] - 10s 45ms/step - loss: 0.0031 - val_loss: 0.0034
Epoch 8/20
219/219 [==============================] - 10s 46ms/step - loss: 0.0032 - val_loss: 0.0028
Epoch 9/20
219/219 [==============================] - 10s 47ms/step - loss: 0.0031 - val_loss: 0.0028
Epoch 10/20
219/219 [==============================] - 10s 47ms/step - loss: 0.0030 - val_loss: 0.0029
Epoch 11/20
219/219 [==============================] - 11s 48ms/step - loss: 0.0029 - val_loss: 0.0027
Epoch 12/20
219/219 [==============================] - 10s 45ms/step - loss: 0.0030 - val_loss: 0.0031
Epoch 13/20
219/219 [==============================] - 10s 45ms/step - loss: 0.0030 - val_loss: 0.0031
Epoch 14/20
219/219 [==============================] - 10s 45ms/step - loss: 0.0030 - val_loss: 0.0030
Epoch 15/20
219/219 [==============================] - 10s 45ms/step - loss: 0.0030 - val_loss: 0.0030
Epoch 16/20
219/219 [==============================] - 10s 46ms/step - loss: 0.0030 - val_loss: 0.0027
Epoch 17/20
219/219 [==============================] - 10s 45ms/step - loss: 0.0029 - val_loss: 0.0028
Epoch 18/20
219/219 [==============================] - 10s 48ms/step - loss: 0.0030 - val_loss: 0.0027
Epoch 19/20
219/219 [==============================] - 10s 44ms/step - loss: 0.0029 - val_loss: 0.0028
Epoch 20/20
219/219 [==============================] - 10s 44ms/step - loss: 0.0029 - val_loss: 0.0026
np.random.seed(43) # 42는 훈련 세트에 있는 첫 번째 시리즈를 반환하기 때문에 다른 값으로 지정합니다
series = generate_time_series(1, n_steps + 10)
X_new, y_new = series[:,:n_steps], series[:,n_steps:]
X=X_new
for step_ahead in range(10):
y_pred = model.predict(X[:,step_ahead:])[:, np.newaxis,:]
X = np.concatenate([X,y_pred],axis=1)
Y_pred = X[:, n_steps:]
def plot_multiple_forecasts(X, Y, Y_pred):
n_steps = X.shape[1]
ahead = Y.shape[1]
plot_series(X[0, :, 0])
plt.plot(np.arange(n_steps, n_steps + ahead), Y[0, :, 0], "bo-", label="Actual")
plt.plot(np.arange(n_steps, n_steps + ahead), Y_pred[0, :, 0], "rx-", label="Forecast", markersize=10)
plt.axis([0, n_steps + ahead, -1, 1])
plt.legend(fontsize=14)
plot_multiple_forecasts(X_new, y_new, Y_pred)
plt.show()
np.mean(keras.losses.mean_squared_error(Y_pred,y_new))
한번에 여러개 예측 (벡터)¶
물론 하나씩 추가하면서 하는 것보다 다음 값 10개를 한번에 예측하는 방식도 있다.
Sequence to vector 모델이지만 값 10개를 출력해준다. (타깃이 10개의 값이 담긴 벡터)
series = generate_time_series(10000, n_steps + 10)
X_train, y_train = series[:7000, :n_steps], series[:7000, -10:, 0]
X_valid, y_valid = series[7000:9000, :n_steps], series[7000:9000, -10:, 0]
X_test, y_test = series[9000:, :n_steps], series[9000:, -10:, 0]
model = keras.models.Sequential([
keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None, 1]),
keras.layers.SimpleRNN(20),
keras.layers.Dense(10)
])
model.compile(loss="mse", optimizer="adam")
model.fit(X_train, y_train, epochs=20, validation_data=(X_valid, y_valid))
y_pred = model.predict(X_test)
np.mean(keras.losses.mean_squared_error(y_test, y_pred))
모든 타임스텝에서 seq 예측¶
마지막 타임 스텝에서 다음 값 10개를 예측하도록 훈련시키는 것 보다
모든 타임 스텝에서 다음 값 10개를 예측하도록 훈련시키면 훈련이 안정적이고 속도가 증가한다.
따라서 seq to seq RNN으로 변경하여 모든 타임 스텝의 출력에 대한 손실이 포함된다.
따라서 타깃 값이 입력에 포함된 값을 가질 수 있지만 타임 스텝마다 모델은 이전 타임 스텝만 볼 수 있다.
이를 인과 모델 (causal model) 이라고 부른다.
np.random.seed(42)
n_steps = 50
series = generate_time_series(10000, n_steps + 10)
X_train = series[:7000, :n_steps]
X_valid = series[7000:9000, :n_steps]
X_test = series[9000:, :n_steps]
Y = np.empty((10000, n_steps, 10))
# 모든 현재 타임 스텝에서 n_steps 만큼 떨어진 값을 예측한다.
for step_ahead in range(1, 10 + 1):
Y[..., step_ahead - 1] = series[..., step_ahead:step_ahead + n_steps, 0]
Y_train = Y[:7000]
Y_valid = Y[7000:9000]
Y_test = Y[9000:]
X_train.shape, Y_train.shape
((7000, 50, 1), (7000, 50, 10))np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None, 1]),
keras.layers.SimpleRNN(20, return_sequences=True),
keras.layers.TimeDistributed(keras.layers.Dense(10))
# TimeDistributed가 각 타임 스텝을 하나의 샘플로 처리하고 Dense층의 입력으로 넣어준다.
# 이후 다시 seq로 묶어서 사용할 수 있도록 출력해준다.
])
def last_time_step_mse(Y_true, Y_pred):
return keras.metrics.mean_squared_error(Y_true[:, -1], Y_pred[:, -1])
model.compile(loss="mse",
optimizer=keras.optimizers.Adam(learning_rate=0.01),
metrics=[last_time_step_mse])
history = model.fit(X_train,
Y_train,
epochs=20,
validation_data=(X_valid, Y_valid))
Epoch 1/20
219/219 [==============================] - 13s 51ms/step - loss: 0.0508 - last_time_step_mse: 0.0400 - val_loss: 0.0429 - val_last_time_step_mse: 0.0324
Epoch 2/20
219/219 [==============================] - 11s 48ms/step - loss: 0.0395 - last_time_step_mse: 0.0283 - val_loss: 0.0352 - val_last_time_step_mse: 0.0245
Epoch 3/20
219/219 [==============================] - 10s 47ms/step - loss: 0.0321 - last_time_step_mse: 0.0208 - val_loss: 0.0292 - val_last_time_step_mse: 0.0171
Epoch 4/20
219/219 [==============================] - 11s 51ms/step - loss: 0.0296 - last_time_step_mse: 0.0184 - val_loss: 0.0272 - val_last_time_step_mse: 0.0151
Epoch 5/20
219/219 [==============================] - 11s 51ms/step - loss: 0.0271 - last_time_step_mse: 0.0150 - val_loss: 0.0270 - val_last_time_step_mse: 0.0172
Epoch 6/20
219/219 [==============================] - 11s 49ms/step - loss: 0.0250 - last_time_step_mse: 0.0122 - val_loss: 0.0220 - val_last_time_step_mse: 0.0088
Epoch 7/20
219/219 [==============================] - 11s 48ms/step - loss: 0.0233 - last_time_step_mse: 0.0106 - val_loss: 0.0236 - val_last_time_step_mse: 0.0103
Epoch 8/20
219/219 [==============================] - 11s 51ms/step - loss: 0.0217 - last_time_step_mse: 0.0088 - val_loss: 0.0212 - val_last_time_step_mse: 0.0085
Epoch 9/20
219/219 [==============================] - 11s 52ms/step - loss: 0.0214 - last_time_step_mse: 0.0085 - val_loss: 0.0199 - val_last_time_step_mse: 0.0070
Epoch 10/20
61/219 [=======>......................] - ETA: 7s - loss: 0.0215 - last_time_step_mse: 0.0089---------------------------------------------------------------------------
KeyboardInterrupt Traceback (most recent call last)
Input In [20], in <cell line: 20>()
14 return keras.metrics.mean_squared_error(Y_true[:, -1], Y_pred[:, -1])
17 model.compile(loss="mse",
18 optimizer=keras.optimizers.Adam(learning_rate=0.01),
19 metrics=[last_time_step_mse])
---> 20 history = model.fit(X_train,
21 Y_train,
22 epochs=20,
23 validation_data=(X_valid, Y_valid))
File ~\anaconda3\lib\site-packages\keras\utils\traceback_utils.py:64, in filter_traceback.<locals>.error_handler(*args, **kwargs)
62 filtered_tb = None
63 try:
---> 64 return fn(*args, **kwargs)
65 except Exception as e: # pylint: disable=broad-except
66 filtered_tb = _process_traceback_frames(e.__traceback__)
File ~\anaconda3\lib\site-packages\keras\engine\training.py:1384, in Model.fit(self, x, y, batch_size, epochs, verbose, callbacks, validation_split, validation_data, shuffle, class_weight, sample_weight, initial_epoch, steps_per_epoch, validation_steps, validation_batch_size, validation_freq, max_queue_size, workers, use_multiprocessing)
1377 with tf.profiler.experimental.Trace(
1378 'train',
1379 epoch_num=epoch,
1380 step_num=step,
1381 batch_size=batch_size,
1382 _r=1):
1383 callbacks.on_train_batch_begin(step)
-> 1384 tmp_logs = self.train_function(iterator)
1385 if data_handler.should_sync:
1386 context.async_wait()
File ~\anaconda3\lib\site-packages\tensorflow\python\util\traceback_utils.py:150, in filter_traceback.<locals>.error_handler(*args, **kwargs)
148 filtered_tb = None
149 try:
--> 150 return fn(*args, **kwargs)
151 except Exception as e:
152 filtered_tb = _process_traceback_frames(e.__traceback__)
File ~\anaconda3\lib\site-packages\tensorflow\python\eager\def_function.py:915, in Function.__call__(self, *args, **kwds)
912 compiler = "xla" if self._jit_compile else "nonXla"
914 with OptionalXlaContext(self._jit_compile):
--> 915 result = self._call(*args, **kwds)
917 new_tracing_count = self.experimental_get_tracing_count()
918 without_tracing = (tracing_count == new_tracing_count)
File ~\anaconda3\lib\site-packages\tensorflow\python\eager\def_function.py:947, in Function._call(self, *args, **kwds)
944 self._lock.release()
945 # In this case we have created variables on the first call, so we run the
946 # defunned version which is guaranteed to never create variables.
--> 947 return self._stateless_fn(*args, **kwds) # pylint: disable=not-callable
948 elif self._stateful_fn is not None:
949 # Release the lock early so that multiple threads can perform the call
950 # in parallel.
951 self._lock.release()
File ~\anaconda3\lib\site-packages\tensorflow\python\eager\function.py:2956, in Function.__call__(self, *args, **kwargs)
2953 with self._lock:
2954 (graph_function,
2955 filtered_flat_args) = self._maybe_define_function(args, kwargs)
-> 2956 return graph_function._call_flat(
2957 filtered_flat_args, captured_inputs=graph_function.captured_inputs)
File ~\anaconda3\lib\site-packages\tensorflow\python\eager\function.py:1853, in ConcreteFunction._call_flat(self, args, captured_inputs, cancellation_manager)
1849 possible_gradient_type = gradients_util.PossibleTapeGradientTypes(args)
1850 if (possible_gradient_type == gradients_util.POSSIBLE_GRADIENT_TYPES_NONE
1851 and executing_eagerly):
1852 # No tape is watching; skip to running the function.
-> 1853 return self._build_call_outputs(self._inference_function.call(
1854 ctx, args, cancellation_manager=cancellation_manager))
1855 forward_backward = self._select_forward_and_backward_functions(
1856 args,
1857 possible_gradient_type,
1858 executing_eagerly)
1859 forward_function, args_with_tangents = forward_backward.forward()
File ~\anaconda3\lib\site-packages\tensorflow\python\eager\function.py:499, in _EagerDefinedFunction.call(self, ctx, args, cancellation_manager)
497 with _InterpolateFunctionError(self):
498 if cancellation_manager is None:
--> 499 outputs = execute.execute(
500 str(self.signature.name),
501 num_outputs=self._num_outputs,
502 inputs=args,
503 attrs=attrs,
504 ctx=ctx)
505 else:
506 outputs = execute.execute_with_cancellation(
507 str(self.signature.name),
508 num_outputs=self._num_outputs,
(...)
511 ctx=ctx,
512 cancellation_manager=cancellation_manager)
File ~\anaconda3\lib\site-packages\tensorflow\python\eager\execute.py:54, in quick_execute(op_name, num_outputs, inputs, attrs, ctx, name)
52 try:
53 ctx.ensure_initialized()
---> 54 tensors = pywrap_tfe.TFE_Py_Execute(ctx._handle, device_name, op_name,
55 inputs, attrs, num_outputs)
56 except core._NotOkStatusException as e:
57 if name is not None:
KeyboardInterrupt: 긴 시퀸스 다루기¶
시퀸스가 길어질수록 많은 타임 스텝에 걸쳐 실행하면서 펼친 RNN이 매우 깊어진다.
이 때문에 그레디언트 소실, 폭주문제가 발생하고 훈련 시간이 길어지거나 불안정해진다.
불안정한 그레디언트¶
보통 심층 신경망에서 사용되던 기법들을 RNN에서 사용하면 이 문제에 대해 접근할 수 있다.
다만,,, 수렴하지 않는 활성화 함수(ReLU)는 오히려 해로워진다. 왜냐면 타임 스텝이 거듭되면서
동일한 가중치가 이용되고 따라서 출력값이 특정한 방향으로 폭줄할 수 있다.
(계속해서 증가하는 방향으로 가중치가 갱신되는 경우)
작은 학습률을 이용하거나 tanh 와 같은 수렴하는 활성화 함수를 사용하는 것이 가장 현실적인 대안이다.
만약 그래도 불안정하면 텐서보드로 모니터링하고 그레디언트 클리핑을 진행하자
배치 정규화가 DNN에서는 효과적이 었지만 RNN에서는 효율적이지 않다.
타임 스텝 사이에 사용할 수 없고 순환 층 사이에서만 이용가능하다는 문제가 있다.
정확히는 메모리 셀에 배치 정규화 층을 추가하여 스텝마다 현재 입력과 이전 은닉 상태 모두 적용할 수 있다만,,,
두 값의 실제 스케일과 상관없이 동일한 파라미터로 하나의 층이 작동되기에 좋은 결과가 나오지 못한다.
이때문에 RNN에서는 층 정규화(Layer Normalization) 이라는 방식을 채택한다.
배치 정규화와 비슷하지만 이 레이어는 특성 차원에 대하여 정규화가 진행된다.
따라서 배치를 어떻게 뽑더라도 통계값이 달라지지 않는다.
층 정규화는 입력과 은닉 상태의 선형 조합 직후에 사용되며 스케일과 이동 파라미터가 하나씩 학습된다.
from tensorflow.keras.layers import LayerNormalization
class LNSimpleRNNCell(keras.layers.Layer):
def __init__(self, units, activation="tanh", **kwargs):
super().__init__(**kwargs)
self.state_size = units
self.output_size = units
self.simple_rnn_cell = keras.layers.SimpleRNNCell(units,
activation=None)
self.layer_norm = LayerNormalization()
self.activation = keras.activations.get(activation)
def get_initial_state(self, inputs=None, batch_size=None, dtype=None):
if inputs is not None:
batch_size = tf.shape(inputs)[0]
dtype = inputs.dtype
return [tf.zeros([batch_size, self.state_size], dtype=dtype)]
def call(self, inputs, states):
# 출력과 은닉상태는 동일하므로 new_sates를 무시해도 좋다,
outputs, new_states = self.simple_rnn_cell(inputs, states)
norm_outputs = self.activation(self.layer_norm(outputs))
return norm_outputs, [norm_outputs]
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.RNN(LNSimpleRNNCell(20),
return_sequences=True,
input_shape=[None, 1]),
keras.layers.RNN(LNSimpleRNNCell(20), return_sequences=True),
keras.layers.TimeDistributed(keras.layers.Dense(10))
])
model.compile(loss="mse", optimizer="adam", metrics=[last_time_step_mse])
history = model.fit(X_train,
Y_train,
epochs=20,
validation_data=(X_valid, Y_valid))
model.summary()
케라스에서 제공되는 모든 RNN cell들은 dropout과 recurrent_dropout 파라미터를 지원한다.
dropout은 입력에 적용되는 드롭아웃 비율이고 recurrent_dropout은 은닉 상태에 대한 드롭아웃 비율이다.
단기 기억 문제¶
RNN을 걸치면서 데이터가 변환되기에 일부 정보들이 매 훈련 스텝 이후 사라진다.
사실상 시간이 지나면 첫 입력의 흔적을 찾아볼 수가 없다. 이를 위해 LSTM 같은 셀들이 이용된다.
LSTM 셀¶
ref : https://dgkim5360.tistory.com/entry/understanding-long-short-term-memory-lstm-kr
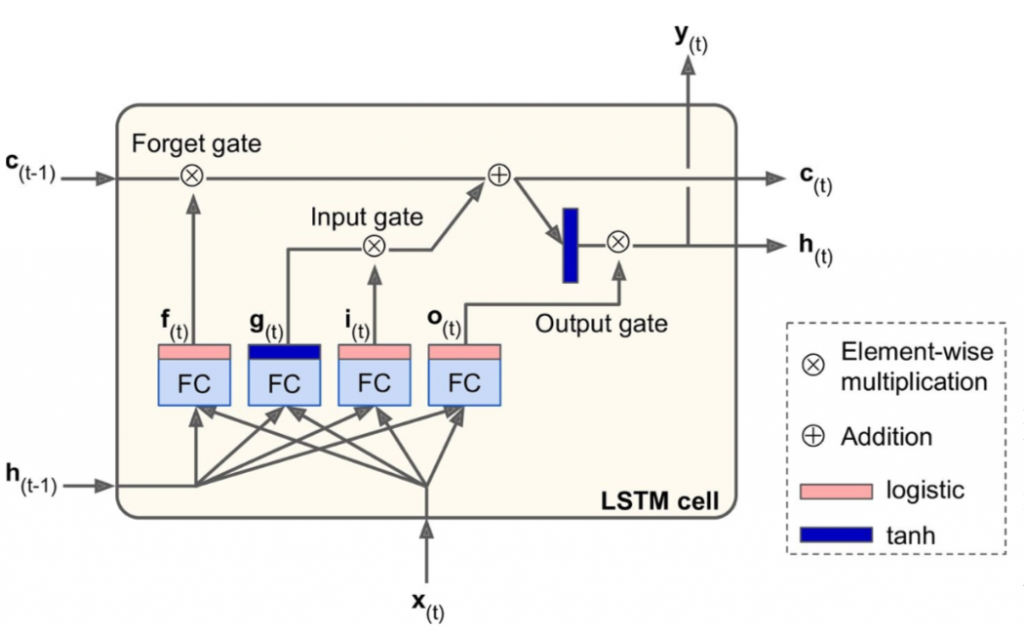
요점은 상태를 장기 기억인 $c_{(t)}$ 와 단기 기억인 $h_{(t)}$ 로 나뉜다는 점이다.
우선 LSTM 셀은 1개의 tanh FC layer와 3개의 sigmoid로 구성된 게이트 제어기로 구성된다.
메인 layer 는 $g_{(t)}$ 를 출력하는 층이다. 이 층은 현재 입력인 $x_{(t)}$ 와 이전의 단기 상태를 분석한다.
$f_{(t)}$ 가 제어하는 삭제 게이트 에서 장기 기억 일부를 잃고
입력 게이트 를 통해서 선택적으로 $g_{(t)}$의 일부를 장기 상태에 추가시킨다. ($i_{(t)}$가 제어)
또한 출력 게이트 를 통해서 현재 스텝에 대한 출력 값과 단기 상태를 제어한다. ($o_{(t)}$가 제어)
식은 다음과 같다 \begin{align*} i_{(t)}& =\sigma(W_{xi}^T x_{(t)}+W_{hi}^T h_{(t-1)}+b_i)\\ f_{(t)}& =\sigma(W_{xf}^T x_{(t)}+W_{hf}^T h_{(t-1)}+b_f)\\ o_{(t)}& =\sigma(W_{xo}^T x_{(t)}+W_{ho}^T h_{(t-1)}+b_o)\\ g_{(t)}& =\tanh(W_{xg}^T x_{(t)}+W_{hg}^T h_{(t-1)}+b_g)\\ c_{(t)}& =f_{(t)}\otimes c_{(t-1)} + i_{(t)}\otimes g_{(t)}\\ y_{(t)}& =h_{(t)} = o_{(t)} \otimes \tanh(c_{(t)}) \end{align*}
$W_{x?}$는 입력 벡터 $x_{(t)}$ 에 대한 가중치 행렬이고 $W_{h?}$는 입력 벡터 $h_{(t-1)}$ 에 대한 가중치 행렬이다.
$b_?$는 4개 층 각각에 대한 편향이며 텐서플로는 $b_f$ 를 0이 아닌 1로 채워진 벡터로 초기화해준다.
# 가장 일반적인 방식 (GPU에서 실행될 때 최적화된 구현을 사용하므로 일반적으로 이용됨)
model = keras.models.Sequential([
keras.layers.LSTM(20, return_sequences=True, input_shape=[None, 1]),
keras.layers.LSTM(20, return_sequences=True),
keras.layers.TimeDistributed(keras.layers.Dense(10))
])
# 범용적인 keras.layers.RNN 층에 LSTMCell을 넣어주는 경우
model = keras.models.Sequential([
keras.layers.RNN(keras.layers.LSTMCell(20),
return_sequences=True,
input_shape=[None, 1]),
keras.layers.RNN(keras.layers.LSTMCell(20), return_sequences=True),
keras.layers.TimeDistributed(keras.layers.Dense(10))
])
GRU 셀¶
Gated Recurrent Unit (GRU) 셀은 LSTM의 간소화 버전이다.

리셋 게이트에서 이전 시점의 hidden state의 값을 얼마나 활용할지 ($r_t$)를 정하고
이 값을 이용하여 업데이트 게이트에서 과거와 현재의 정보를 현재 출력에 얼마나 반영할지를 비율을 정한다.
keras.layers.GRU() # keras.layers.SimpleRNN, LSTM과 동일
keras.layers.GRUCell() # 범용 keras.layers.RNN layer에 넣을 때 사용
Conv1D를 사용한 시퀸스 줄이기¶
Conv1D layer를 사용할 경우, 커널이 슬라이딩하여 1D 특성맵을 출력하여 준다.
스트라이드 1과 "same"을 이용한다면 출력값의 길이와 입력값의 길이가 같겠지만
1보다 큰 스트라이드와 "valid" 패딩을 이용한다면 출력값의 길이가 짧아진다.
이를 사용하여 시퀸스 길이를 줄여주면 RNN의 층들이 더 긴 패턴을 감지하는 데 도움이 된다.
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Conv1D(filters=20, kernel_size=4, strides=2, padding="valid",
input_shape=[None, 1]),
keras.layers.GRU(20, return_sequences=True),
keras.layers.GRU(20, return_sequences=True),
keras.layers.TimeDistributed(keras.layers.Dense(10))
])
model.compile(loss="mse", optimizer="adam", metrics=[last_time_step_mse])
history = model.fit(X_train, Y_train[:, 3::2], epochs=20,
validation_data=(X_valid, Y_valid[:, 3::2]))
Epoch 1/20
219/219 [==============================] - 8s 9ms/step - loss: 0.0681 - last_time_step_mse: 0.0601 - val_loss: 0.0477 - val_last_time_step_mse: 0.0396
Epoch 2/20
219/219 [==============================] - 2s 7ms/step - loss: 0.0414 - last_time_step_mse: 0.0340 - val_loss: 0.0367 - val_last_time_step_mse: 0.0285
Epoch 3/20
219/219 [==============================] - 2s 7ms/step - loss: 0.0338 - last_time_step_mse: 0.0257 - val_loss: 0.0307 - val_last_time_step_mse: 0.0218
Epoch 4/20
219/219 [==============================] - 2s 7ms/step - loss: 0.0282 - last_time_step_mse: 0.0184 - val_loss: 0.0259 - val_last_time_step_mse: 0.0152
Epoch 5/20
219/219 [==============================] - 1s 7ms/step - loss: 0.0249 - last_time_step_mse: 0.0143 - val_loss: 0.0246 - val_last_time_step_mse: 0.0141
Epoch 6/20
219/219 [==============================] - 1s 7ms/step - loss: 0.0234 - last_time_step_mse: 0.0125 - val_loss: 0.0227 - val_last_time_step_mse: 0.0115
Epoch 7/20
219/219 [==============================] - 2s 7ms/step - loss: 0.0226 - last_time_step_mse: 0.0117 - val_loss: 0.0225 - val_last_time_step_mse: 0.0116
Epoch 8/20
219/219 [==============================] - 1s 7ms/step - loss: 0.0220 - last_time_step_mse: 0.0111 - val_loss: 0.0216 - val_last_time_step_mse: 0.0105
Epoch 9/20
219/219 [==============================] - 1s 7ms/step - loss: 0.0216 - last_time_step_mse: 0.0108 - val_loss: 0.0217 - val_last_time_step_mse: 0.0109
Epoch 10/20
219/219 [==============================] - 1s 7ms/step - loss: 0.0213 - last_time_step_mse: 0.0106 - val_loss: 0.0210 - val_last_time_step_mse: 0.0102
Epoch 11/20
219/219 [==============================] - 2s 7ms/step - loss: 0.0210 - last_time_step_mse: 0.0102 - val_loss: 0.0208 - val_last_time_step_mse: 0.0100
Epoch 12/20
219/219 [==============================] - 1s 7ms/step - loss: 0.0208 - last_time_step_mse: 0.0102 - val_loss: 0.0208 - val_last_time_step_mse: 0.0102
Epoch 13/20
219/219 [==============================] - 1s 7ms/step - loss: 0.0205 - last_time_step_mse: 0.0098 - val_loss: 0.0206 - val_last_time_step_mse: 0.0101
Epoch 14/20
219/219 [==============================] - 1s 7ms/step - loss: 0.0204 - last_time_step_mse: 0.0099 - val_loss: 0.0204 - val_last_time_step_mse: 0.0099
Epoch 15/20
219/219 [==============================] - 2s 7ms/step - loss: 0.0202 - last_time_step_mse: 0.0097 - val_loss: 0.0199 - val_last_time_step_mse: 0.0093
Epoch 16/20
219/219 [==============================] - 1s 7ms/step - loss: 0.0200 - last_time_step_mse: 0.0097 - val_loss: 0.0201 - val_last_time_step_mse: 0.0095
Epoch 17/20
219/219 [==============================] - 1s 7ms/step - loss: 0.0196 - last_time_step_mse: 0.0093 - val_loss: 0.0197 - val_last_time_step_mse: 0.0091
Epoch 18/20
219/219 [==============================] - 1s 7ms/step - loss: 0.0194 - last_time_step_mse: 0.0090 - val_loss: 0.0192 - val_last_time_step_mse: 0.0086
Epoch 19/20
219/219 [==============================] - 2s 7ms/step - loss: 0.0190 - last_time_step_mse: 0.0087 - val_loss: 0.0188 - val_last_time_step_mse: 0.0084
Epoch 20/20
219/219 [==============================] - 1s 7ms/step - loss: 0.0186 - last_time_step_mse: 0.0083 - val_loss: 0.0184 - val_last_time_step_mse: 0.0080
WaveNet¶
2016년에 발표된 WaveNet은 층마다 뉴런의 입력이 떨어져 있는 간격인 팽창 비율(dilation rate) 을
2배로 눌리는 1D 합성곱 층을 쌓는다. 그 덕분에 하위 층은 단기 패턴 을 상위층은 장기 패턴 을 학습한다.
덕분에 시퀸스가 아무리 길더라도 효율적으로 처리할 수 있으며 뿐만 아니라 1,2,4,8...,512의 팽창 비율을 가지는
합성곱 층 10개를 하나의 팽창 층(dilated Conv)으로 두고 총 30개를 잔차 블록으로 연결했다.


이런 WaveNet 논문은 텍스트 투 스피치 작업을 포함하여 여러 오디오 문제에서 좋은 성능을 달성했다.
'AI' 카테고리의 다른 글
| [Docker] 기본 명령어 정리 (0) | 2022.07.09 |
|---|---|
| [PyTorch] 모델 설계 및 전이 학습 (0) | 2022.07.05 |
| [핸즈온 머신러닝] chapter 14. 합성곱 신경망 (0) | 2022.05.18 |
| [핸즈온 머신러닝] chapter 13. 텐서플로에서의 데이터 적재와 전처리 (0) | 2022.05.04 |
| [핸즈온 머신러닝] chapter 12. 텐서플로에서의 사용자 정의 모델과 훈련 (0) | 2022.04.28 |
- Total
- Today
- Yesterday
